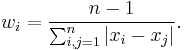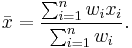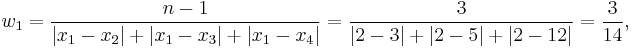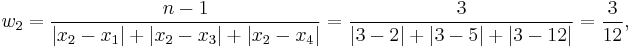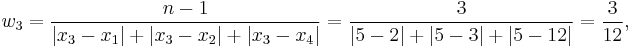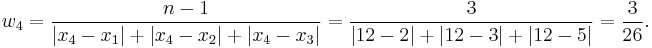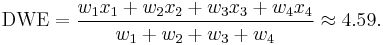Distance-weighted estimator

In statistics, the distance-weighted estimator (the distance-weighted mean) is a measure of central tendency, a special case of weighted mean, where weighting coefficient for each data point is computed as the inverse mean distance between this data point and the other data points. Thus, central observations in a dataset get the highest weights, while values in the tails of a distribution are downweighted. In other words, data points close to other data points carry more weight than isolated datapoints.

An important property of the distance-weighted estimator is that computing weighting coefficients does not require mean or other parameters of the original distribution as input information, because each value in the dataset is weighted in relation to the entire data array.

1 Calculation
- 1.1 Example
- 1.2 The R code for computing the distance-weighted mean
2 Comparison to other measures of central tendency
3 References

Calculation

The weighting coefficient for x_i is computed as the inverse mean distance between x_i and the other data points:

$w_i = \frac{n-1}{\sum_{i,j=1}^n |x_i-x_j|}.$

These coefficients are next substituted into the general formula of weighted mean:

$\bar{x} = \frac{ \sum_{i=1}^n w_i x_i}{\sum_{i=1}^n w_i}.$

Note: weighting coefficients could be calculated as a simple sum instead of an average of the distances, but in certain cases (e.g., large sums of distances) this would result in a lower accuracy in the calculations.

Example

Consider a simple numerical example of a dataset consisting of four observations: x₁ = 2, x₂ = 3, x₃ = 5, x₄ = 12 (n = 4). Weighting coefficients for x_i are:

$w_1 = \frac{n-1}{\left| {x_1-x_2} \right| %2B \left| {x_1-x_3} \right| %2B \left| {x_1-x_4} \right|} = \frac{3}{\left| {2-3} \right| %2B \left| {2-5} \right| %2B \left| {2-12} \right|} = \frac{3}{14},$

$w_2 = \frac{n-1}{\left| {x_2-x_1} \right| %2B \left| {x_2-x_3} \right| %2B \left| {x_2-x_4} \right|} = \frac{3}{\left| {3-2} \right| %2B \left| {3-5} \right| %2B \left| {3-12} \right|} = \frac{3}{12},$

$w_3 = \frac{n-1}{\left| {x_3-x_1} \right| %2B \left| {x_3-x_2} \right| %2B \left| {x_3-x_4} \right|} = \frac{3}{\left| {5-2} \right| %2B \left| {5-3} \right| %2B \left| {5-12} \right|} = \frac{3}{12},$

$w_4 = \frac{n-1}{\left| {x_4-x_1} \right| %2B \left| {x_4-x_2} \right| %2B \left| {x_4-x_3} \right|} = \frac{3}{\left| {12-2} \right| %2B \left| {12-3} \right| %2B \left| {12-5} \right|} = \frac{3}{26}.$

The distance-weighted estimator is:

$\mathrm{DWE} = \frac{w_1 x_1 %2B w_2 x_2 %2B w_3 x_3 %2B w_4 x_4}{w_1 %2B w_2 %2B w_3 %2B w_4} \approx 4.59.$

The R code for computing the distance-weighted mean

GeSHi Error: GeSHi could not find the language rsplus (using path /usr/share/php-geshi/geshi/) (code 2)

You need to specify a language like this: <source lang="html4strict">...</source>

Supported languages for syntax highlighting:

abap, actionscript, actionscript3, ada, apache, applescript, apt_sources, asm, asp, autoit, avisynth, bash, basic4gl, bf, bibtex, blitzbasic, bnf, boo, c, c_mac, caddcl, cadlisp, cfdg, cfm, cil, cmake, cobol, cpp, cpp-qt, csharp, css, d, dcs, delphi, diff, div, dos, dot, eiffel, email, erlang, fo, fortran, freebasic, genero, gettext, glsl, gml, gnuplot, groovy, haskell, hq9plus, html4strict, idl, ini, inno, intercal, io, java, java5, javascript, kixtart, klonec, klonecpp, latex, lisp, locobasic, lolcode, lotusformulas, lotusscript, lscript, lsl2, lua, m68k, make, matlab, mirc, modula3, mpasm, mxml, mysql, nsis, oberon2, objc, ocaml, ocaml-brief, oobas, oracle11, oracle8, pascal, per, perl, php, php-brief, pic16, pixelbender, plsql, povray, powershell, progress, prolog, properties, providex, python, qbasic, rails, rebol, reg, robots, ruby, sas, scala, scheme, scilab, sdlbasic, smalltalk, smarty, sql, tcl, teraterm, text, thinbasic, tsql, typoscript, vb, vbnet, verilog, vhdl, vim, visualfoxpro, visualprolog, whitespace, whois, winbatch, xml, xorg_conf, xpp, z80

Comparison to other measures of central tendency

Distance-weighted mean is less sensitive to outliers than the mean and many other measures of central tendency. It can be regarded as an alternative to trimmed mean and Winsorized mean ^[1]. The main advantage of the distance-weighted estimator is that it does not require definite judging of whether or not some values must be deleted as outliers, which is extremely important for empirical studies when no data point can be identified as an outlier with confidence.

References

^ Yury S. Dodonov, & Yulia A. Dodonova Robust measures of central Tendency: weighting as a possible alternative to trimming in response-time data analysis